Starý, za socializmu zakázaný vtip o sovietskych protivzdušných systémoch hovoril, že dokázali otočiť hocijakú americkú raketu a to o nie o úbohých 180, ale dokonca až o 360 stupňov.

Prečo má kruh 360 stupňov?

Ako mnohé veci týkajúce sa matematiky a obzvlášť geometrie, aj tu sa musíme pozrieť hlboko do histórie a to konkrétne k starovekým Babylončanom. Tí boli prví, ktorí rozdelili kruh na 360 rovnakých dielikov a pravdepodobne sa tak stalo okolo roku 2400 pred Kristom. Rozdelenie je teda staré 4500 rokov a bolo také geniálne, že ani moderná matematika nemala potrebu v tom niečo meniť, ako píše IFL Science.

Ak by sme ale mali pristúpiť na vysvetlenie tohto rozdelenia, to je už trošku náročnejšie. Pravdou je, že s istotou nevieme povedať, prečo Babylončania kruh rozdelili na 360 stupňov, to ale neznamená, že neexistujú hypotézy, ktoré by sa to nepokúšali vysvetliť.

Astronomický dôvod

Babylončanov fascinovali hviezdy a nočná obloha. Tak ako aj dnes sa na ne odvoláva astrológia a pochybné horoskopy, tak aj Babylončania vo hviezdach videli znamenia a to, ako sa bude meniť ich osud podľa polôh planét a iných nebeských telies vzhľadom k nim.

Pre dobré mapovanie oblohy ale potrebujete kvalitný zápis. Keďže nočná obloha sa pre pozorovateľa javí ako kruh, tento objekt bol základ pre ich zakresľovanie. Jeho rozdelenie na 360 dielikov môže zodpovedať jednému roku a teda pohybu Slnka po oblohe. Jeden deň tak mohol znamenať jeden stupeň a jedno pohnutie Slnka vzhľadom k hviezdam. Keď Slnko prejde spomínaných 360 stupňov, vráti sa na svoju pôvodnú pozíciu.

Rozdeľovanie je jednoduchšie

Astronomická hypotéza by to celé mohla vysvetľovať, no existuje aj ďalšia hypotéza, ktorá nevylučuje tú prvú. Pri pohľade na matematiku Babylončanov vidíme oproti tej súčasnej jeden veľký rozdiel.

Kým my používame ako základ čísiel desatinnú sústavu, Babylončania používali šesťdesiatkovú sústavu, kde nebolo základné číslo 10, ako u nás, ale 60.

Aj keď pre nás to môže vyznievať divne, na jej používanie prevláda silný argument. „Dôvod používania čísla 60 je nejasný, ale mohlo to byť tak, že číslo 60 sa dá veľmi dobre deliť množstvom malých celých čísiel bez zvyškov, či bez používania zlomkov,“ vysvetlil Chris Linton, profesor aplikovanej matematiky na univerzite v anglickom meste Loughborough, vo svojej knihe z roku 2004 From Eudoxus to Einstein: A History of Mathematical Astronomy.

Je to naozaj logické. Kým číslo 60 môžete bez zvyšku deliť mnohými malými číslami ako dvojkou, trojkou, štvorkou, šestkou či desiatkou, tak číslo 10 bez zvyšku delíte iba dvojkou, päťkou a desiatkou. Pre Babylončanov tak bolo delenie jednoduché.

A ak je 60 fajn číslo, tak jeho vynásobenie šestkou je ešte lepšie. Číslo 360 sa dá deliť až 24 číslami tak, aby nezostal žiadny zvyšok. A táto vlastnosť je skvelá nielen na papieri, ale najmä v aplikovaní.

Skúste si napríklad rozdeliť zemeguľu na 24 časových pásiem pomocou 100-stupňového základu. Budete mať časové pásmo o veľkosti 4,16666… stupňov zemepisnej dĺžky, čo je mimoriadne nepraktické a v presných meraniach absolútne nevhodné. S 360 stupňami sa ale dostávate na 15 stupňov zemepisnej dĺžky na jedno časové pásmo.

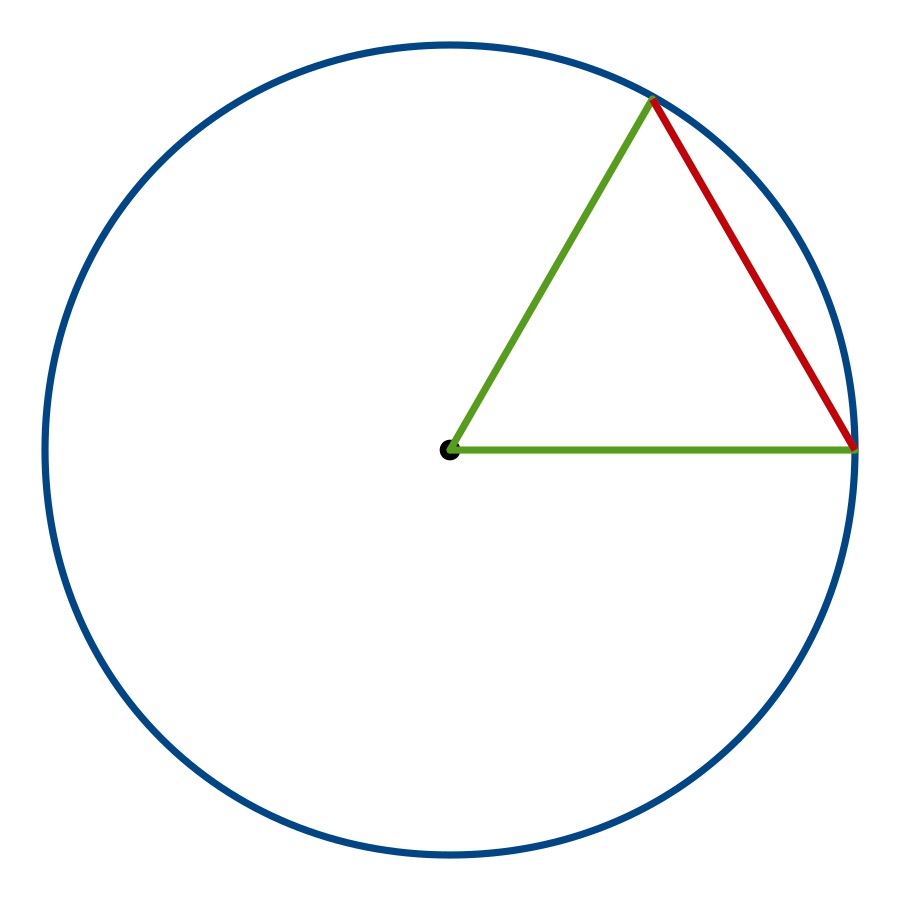
Prečo ale číslo 60 násobili šiestimi? Tu nám môžu pomôcť starovekí grécki matematici, ktorí sa tiež inšpirovali Babylončanmi. Grécki matematici boli fascinovaní trojuholníkmi. Ak si zoberiete kruh a vpíšete doň rovnostranný trojuholník o dĺžke strany rovnajúcej sa polomeru kruhu (a uhlom 60 stupňov), tak takýchto rovnakých trojuholníkov vpíšete do kruhu presne 6, čím ho vyplníte. 60 sa tak prirodzene stáva základom pre svet geometrie.

Nie vždy sú stupne vhodné

Samozrejme, aj stupne majú svoje limity pri výpočtoch. Ak sa bavíme o základnej geometrii a matematike, dá sa operovať so stupňami. No je tu jedno iracionálne, ale mimoriadne dôležité číslo a tým je π. Kým na základnej škole sa pre zjednodušenie používalo iba 3,14, v skutočnosti ide o nekonečný rad čísiel a pri komplexnejšej matematike sa musí pracovať s π.

A keďže všetky vzorce týkajúce sa kruhových objektov obsahujú π, je potrebné s ním rátať aj pri počítaní uhlov. Bola preto zavedená jednotka radián, ktorú používali v stredoveku islamskí matematici.(V celom kruhu sa nachádza radiánov 2π).

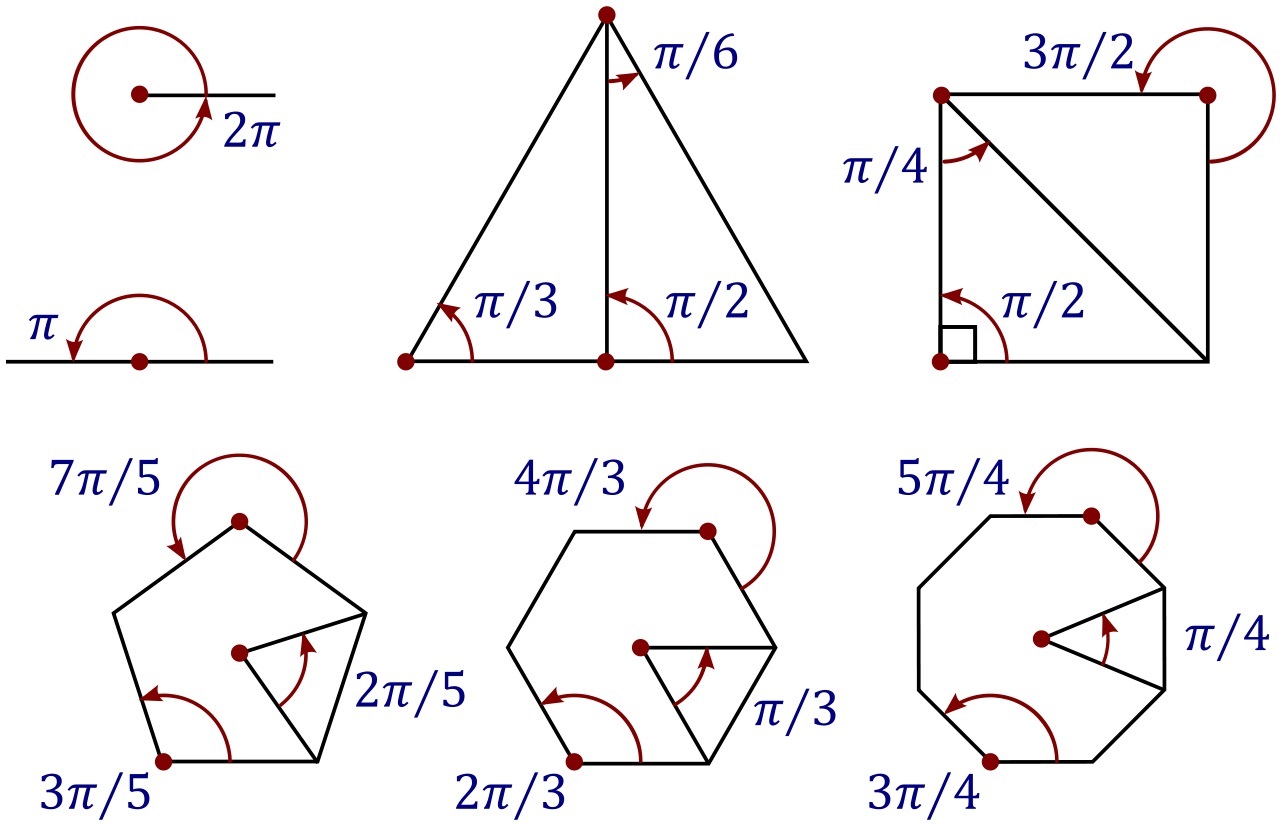
Radián je z matematického hľadiska vhodnejší a prirodzenejší, lebo poskytuje presné výsledky a de facto zjednodušuje výpočty, ktoré by inak boli divné a nezrozumiteľné pri používaní uhlov. Niekedy je teda vhodnejšie, či priam nutné, najmä pri diferenciálnom počte, používať radiány.

Dôležité sú teda aj radiány, a tiež aj stupne, najmä pri jednoduchej matematike. A tiež by ani úvodný vtip nebol veľmi zábavný, ak by sa v ňom otáčala raketa nie o 360 stupňov ale o 2π.

Pozri aj:

Maturita 2023: Zvládli by ste dnešný test z matematiky? Otestujte sa!