Pytagorova veta je jedným zo základných vzorcov matematiky a aj tí, ktorí tento predmet v škole veľmi neobľubovali, jej definíciu vedeli naspamäť a vedeli ju aj používať. Avšak nájsť dôkaz Pytagorovej vety pomocou trigonometrie, keďže samotná Pytagorova veta predstavuje jej základ, sa javí ako nemožné. No dve stredoškoláčky to, zdá sa, dokázali. 

Pytagorova veta je stará tisícročia, a aj keď je pomenovaná po slávnom učencovi Pytagorovi zo Sámosu, ktorý ju odvodil, je pravdepodobné, že iné civilizácie, napríklad starí Egypťania a Indovia ju využívali už pred 4 000 rokmi, ako uvádza IFL Science.

Dôkaz na sínusovej vete

Aj keď existuje mnoho dôkazov Pytagorovej vety, tie vychádzajú práve z Pytagorovej vety. Dve stredoškoláčky, Ne’Kiya Jacksonová a Calcea Rujean Johnsonová, 18. marca 2023 na zasadnutí Americkej matematickej spoločnosti v prednáške predstavili dôkaz Pytagorovej vety, ktorý je založený na sínusovej vete, ktorý je nezávislý od Pytagorovej vety.

„Je ťažké prísť na nové nápady v tak dobre prebádanej oblasti, ako je táto veta, takže som nadšený, že na to prišli dve stredoškoláčky,“ uvádza YouTuber MathTrain, ktorý sa pokúsil vysvetliť, ako dievčatá na dôkaz prišli. Samotný dôkaz ešte totiž nebol zverejnený, a tak sa YouTuber pokúsil nájsť dôkaz na základe toho, čo videl z fotiek z prednášky.

Najprv si pripomeňme samotnú Pytagorovu vetu. Tá hovorí to, že ak máme pravouhlý trojuholník, tak obsah štvorca zostrojeného nad preponou je rovný súčtu obsahov štvorcov zostrojených nad jeho odvesnami. Zápis tohto vzťahu vyzerá takto: a² + b² = c^2.

Len veľmi málo dôkazov sa spolieha na trigonometriu. Johnsonová a Jacskonová však tvrdia, že existuje jedna výnimka, a to je sínusova veta. Tá hovorí, že pre každý trojuholník platí nasledujúci vzťah:

Dôkaz vety

Výhodou je, že táto veta je pravdivá nezávisle na Pytagorovej vete a mohla byť použitá ako základ na jej dokázanie. MathTrain sa pokúsil napodobniť postup stredoškoláčok. Najprv si zostrojil pravouhlý trojuholník a označil strany a uhly. Akýsi štandardný postup, ak by ste chceli dokázať Pytagorovu vetu.

V ďalšom kroku pridal ďalšie trojuholníky — najprv ten pôvodný zdvojnásobil pridaním zrkadlového obrazu na jednu stranu, potom predĺžil preponu zrkadlového trojuholníka, až kým sa nespojila s priamkou kolmou na pôvodnú preponu. Výsledkom je nový pravouhlý trojuholník, ale kľúč k odpovedi nespočíva v ňom, ale v menších trojuholníkoch, ktoré ho vypĺňajú.

Poslednou časťou je totiž rozdelenie veľkého trojuholníka na nekonečne veľa menších pravouhlých trojuholníkov, ktoré sú podobné originálu. Keď sa spočítajú odvesny a prepony nekonečne malých trojuholníkov, dostávame sa do sveta geometrických radov.

Ak sa podobným spôsobom vykoná aj výpočet Z, ako je na obrázku vyššie, dostaneme výsledok:

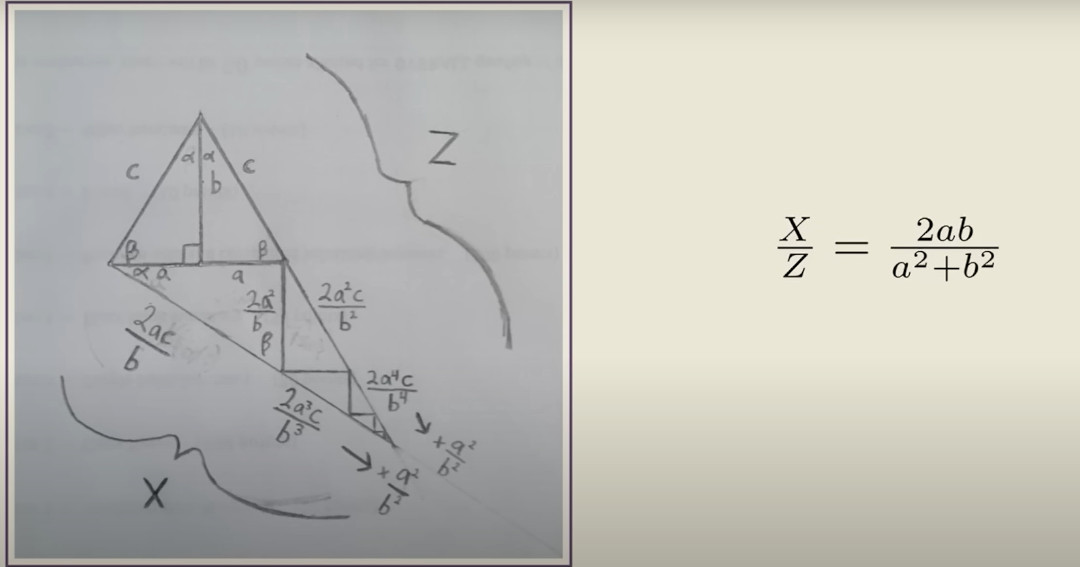
Konečne prichádza na rad sínusová veta. Keďže vieme, že sínus pomeru X a Z sa rovná sin (2A) a použitím sínusovej vety na trojuholník vytvorený originálnym pravouhlým trojuholníkom a na jeho zrkadlový obraz, dostávame niečo, čo už vyzerá ako Pytagorova veta:

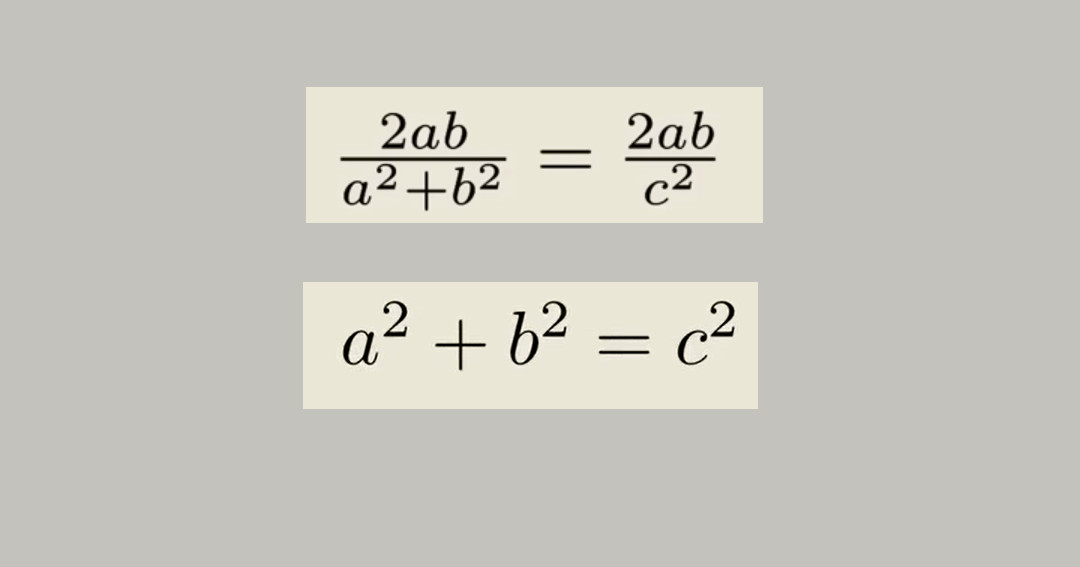
Nie je jasné, či takýto postup zvolili aj stredoškoláčky, ale YouTuber predpokladá, že to mohlo byť takto. Samozrejme, tento dôkaz Pytagorovej vety ešte nie je platný, kým nebude recenzovaný a uznaný.

Americká matematická spoločnosť oslavuje obidve študentky a podporujú ich v ďalšom štúdiu matematiky. Johnsonová a Jacksonová sú zo svojho úspechu nadšené a hovoria, že nie je časté vidieť, že s takýmito riešeniami prichádzajú deti ako ony, ale bývajú to dospelí ľudia.

Pozri aj:

Viete, koľko je 550 ÷ 2? Jednoduchý matematický príklad sa stal virálnym a ľudia sa…