Škola MIT je jednou z najprestížnejších technologických univerzít v USA. Dostať sa na ňu je poriadne náročné, avšak ten, kto školu vyštuduje, má v podstate otvorené brány v každej firme so zameraním, ktoré vyštudoval. Škola funguje od roku 1861 a o pár dní oslávi 160 rokov svojho fungovania.
správy od nás budete mať ako prví.
Asi vás neprekvapí, že v čase vzniku školy alebo aj trochu neskôr, napríklad pred 150 rokmi, neboli prijímacie skúšky také náročné, aké sú dnes. Na druhej strane, aj vtedy ste potrebovali vedieť a rozumieť geometrii, algebre či aritmetike, informuje IFL Science.
Ako by ste si poradili s touto otázkou?
Po internete kolujú viaceré otázky, ktoré sa používali na prijímacie skúšky v minulosti. Jedna z nich je nasledovná:
Kolmica smeruje z pravého uhla pravouholníka na preponu a rozdeľuje ho na dva trojuholníky, v ktorých je pôvodná prepona rozdelená na strany o dĺžke 9 a 16. Určte dĺžku kolmice a ostatných strán dvoch trojuholníkov.
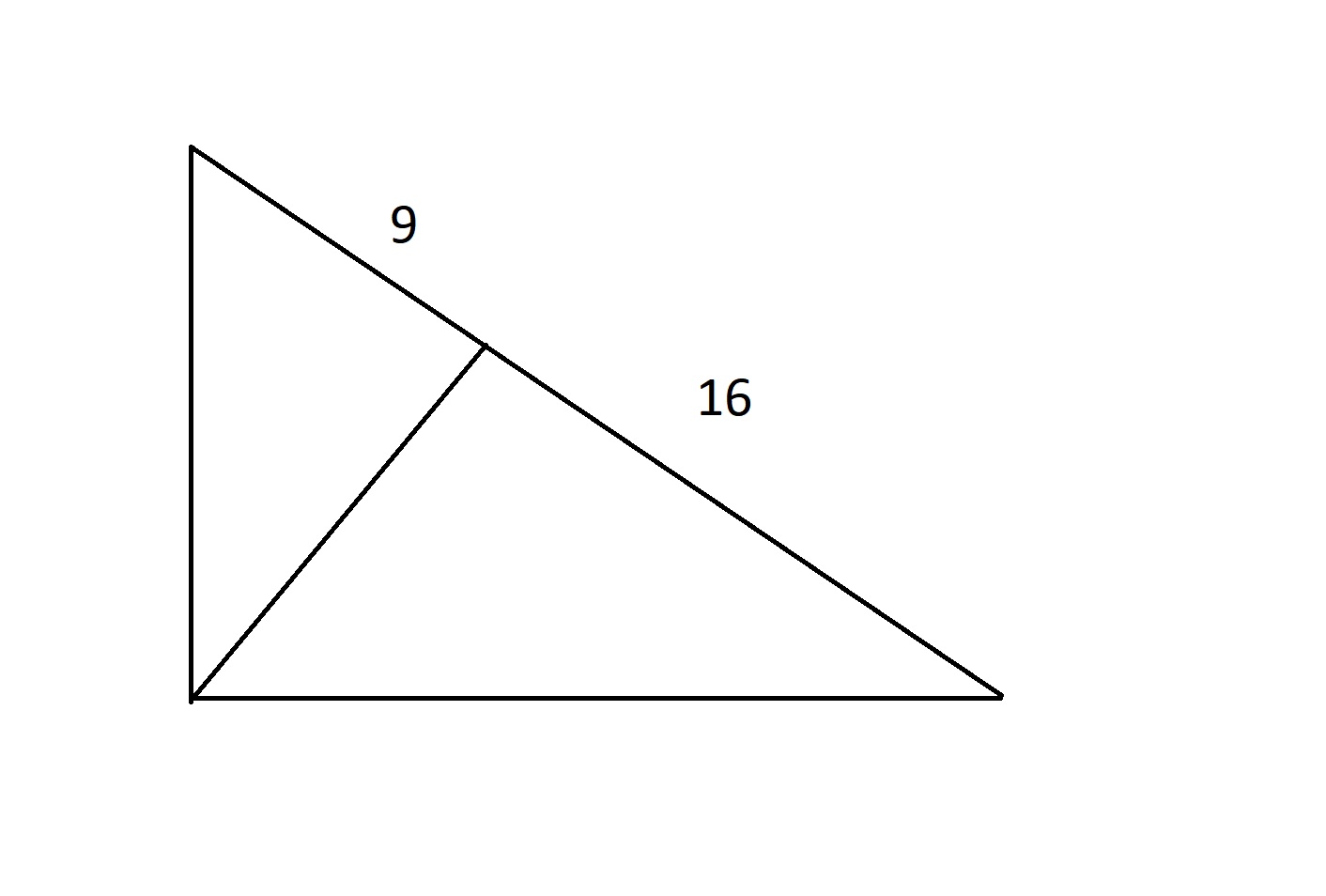
Riešenie
Výsledok poskytuje Mind Your Decisions:
Trojuholníky sú si veľmi podobné a pomer kratšej a dlhšej strany sú si podobné.
Je teda možné počítať takto:
CD / AD = AD / BD
9 / p = p / 16
9 (16) = p 2
144 = p 2
p = 12 (bez záporného koreňa)
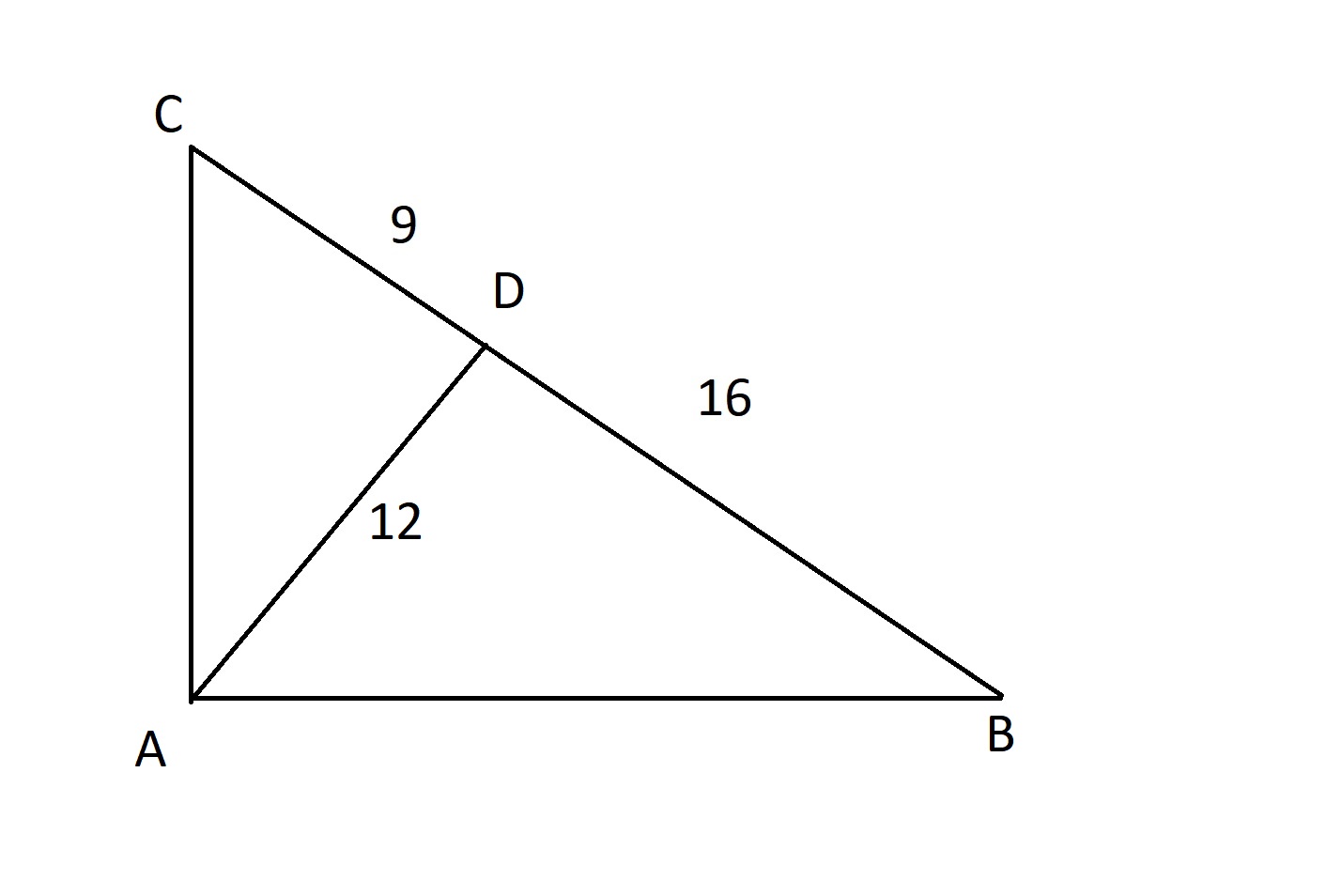
Následne je možné uplatniť Pytagorovu vetu. Môžeme si tiež pomôcť rýchlejším výpočtom, keďže strany sú si pomerné. Jeden z trojuholníkov má odvesny 9 a 12, znamená to, že prepona bude dlhá 15. Druhý trojuholník má odvesny dlhé 12 a 16, čo znamená, že prepona má dĺžku 20.
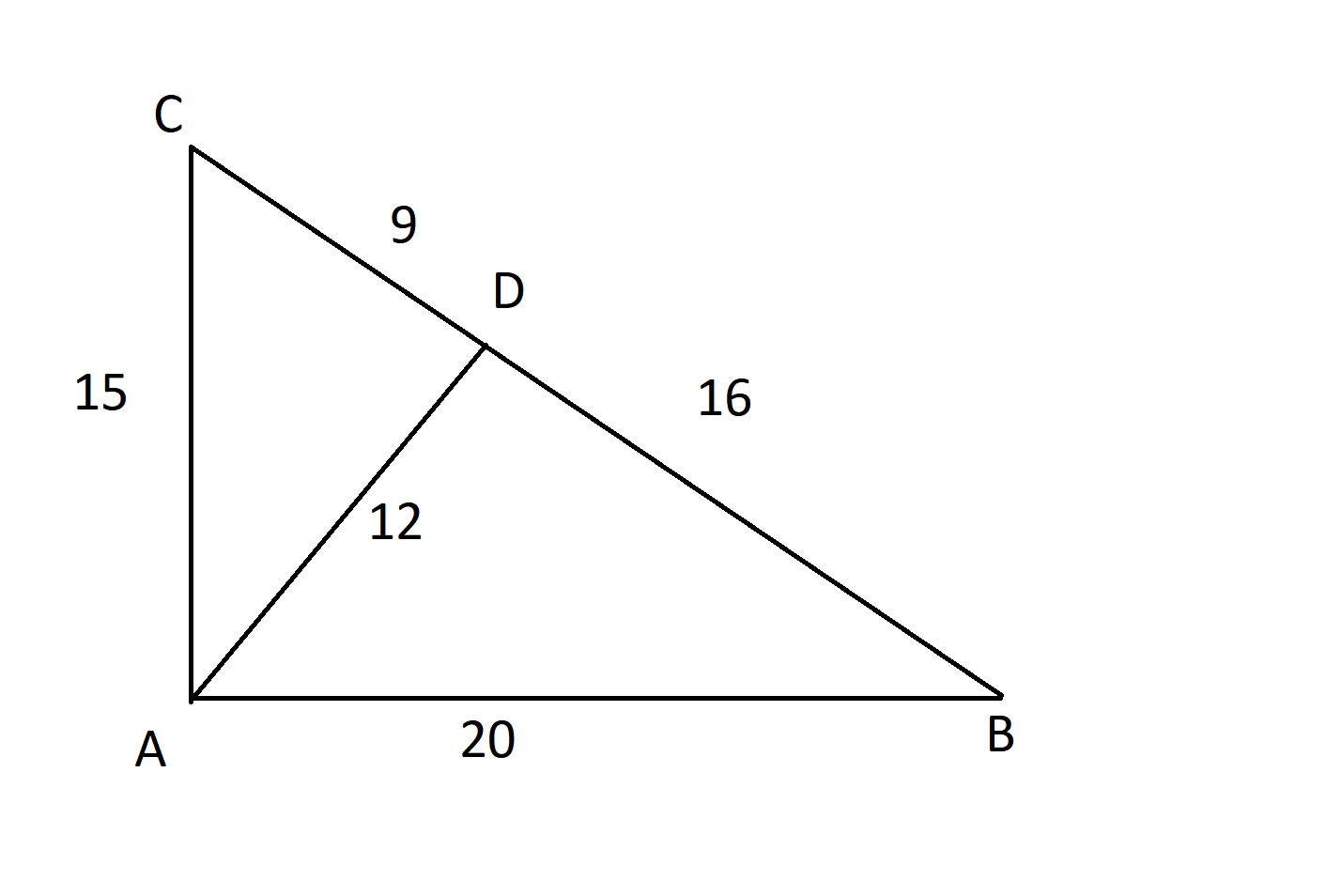
Môžete si tiež pozrieť video od Mind Your Decisions (v angličtine), ktoré príklad a postup vysvetľuje.
Nahlásiť chybu v článku